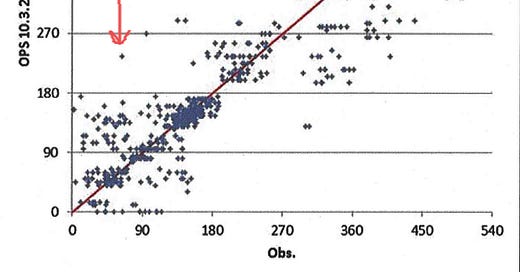
Take a look-see at the science pic above.
This is the output from some model, the nature of which is not especially interesting, and the accompanying observations. In other words, predictions and the resulting values.
See the red arrow? I picked this point because it's easy to see; there is nothing else special about it.
The blue diamond the arrow highlights was an instance at which the model said, "The value will be 240" (or whatever). But the observation was 70 (or so).
Very well: the model said 240 and Nature said 70. The model is therefore falsified. The model said a thing would happen. It did not happen. The model has said a false thing. The model was wrong: it was not right. It is falsified, so throw the model out. Right?
We have discussed the philosophy of falsifiability in detail before. Today, I want to speak of the sociology of it. Do not mix them up; however, the latter relies, in part, on the former, so we can't entirely separate them.
Next cast your eye to the other blue diamonds. Sometimes the model said what would happen, or near enough, and sometimes the model did not. The model has been falsified not only once, but many times: indeed, each time the blue diamond does not fall on the red 1-to-1 line the model has been falsified again.
Now to the sociol----
"---Wait, Briggs. Nobody takes the predicted values perfectly serious."
What do you mean?
"I mean that when the model says '240,' everybody takes that to mean '240 plus or minus a little.'"
So that if the observation goes outside that "little", the model is then falsified?
"Not quite. Because most other predictions, the whole of those blue diamonds, might be close enough."
How many have to be "close enough"?
"It depends."
Sounds pretty vague and subjective, this falsifiability. It only works when you say it does, based on rules that can't be communicated quantitatively.
It also sounds like you mean that, in math, we can work out that each model prediction is "ackshually" a probability, like the mean of a normal distribution, or whatever. But that implies adding another model on the original model, a probability model (if the model itself doesn't have this feature). Then each prediction is given a non-zero probability of happening. That 240 might have been given a probability of, say, 10%. It turned out to be 70, which the model gave a probability of, say, 0.1% to.
In other words, the model said the 70 was possible: 70 happened. The model is not falsified. So we can keep it.
But then, no observation can ever contradict the model, not formally. Because the probability model will never say any point is impossible.
Formally, falsifiability is useless.
Now let's turn it around and look at a model that I say has had enough evidence of its failure, one so bad that no earnest person can believe it. A model that has had a century's worth of dismal performance, which has never worked anywhere in practice. Yet which is still believed---and even cherished!
I call this model Masks Stop The Spread Of Respiratory Diseases, or Masks for short. Hard to find an Expert or ruler who isn't a True Believer in Masks. Here's a fun picture:

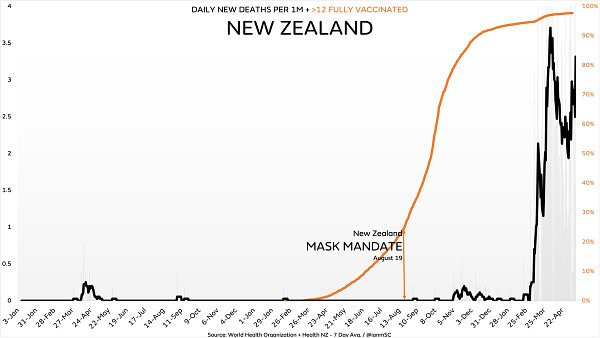
This fellow has dozens upon dozens of pictures like this; others contrasting areas with mask mandates with those that don't. Usually, the areas without mandates do better, in the sense of lower deaths or infections (mistakenly called "cases"). I haven't seen any pics where maskless areas obviously do worse.
I have dozens of old studies, including the time when surgeons stopped wearing masks in a busy hospital for six weeks and there was no change in infection rates, all starting from a century ago, all showing the uselessness of Masks. Further, this information is easy to find, and easy to read, especially with those who have any training in medicine or statistics, and so should not be a mystery to anybody.
As far as falsifying a model goes, Masks has been as falsified as it can get.
Yet I ask you: is Masks still believed? Do elites, Experts and rulers still laud and praise it?
And why? Ah, that's the real answer. Because any model that's useful is a good model, falsifiability be damned. Both models detailed today are useful---to certain people. The trick is understanding that the model doesn't have to be useful for the things of which it speaks. It merely need be a device to point to to justify an action one desires.
For the first model, it's agriculture. For the second, it's health. Both models exist for governments to say "We are doing something. And that something is The Science." The simple models become meta models, part of a larger scheme. It's those meta models that need examination.
The only conclusion is: however valuable it is in rigorous formal logic and mathematics, falsifiability is useless in science. Don't bother with it.
Buy my new book and learn to argue against the regime: Everything You Believe Is Wrong.
Visit wmbriggs.com.



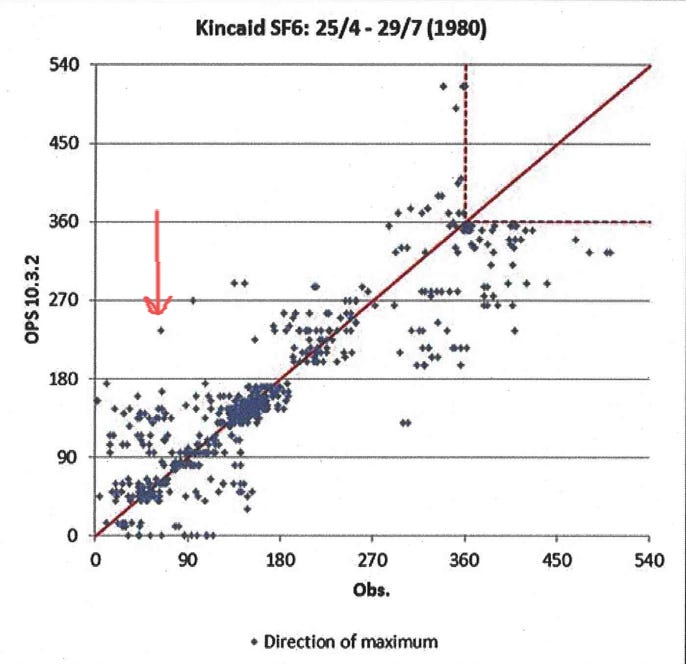
I publish and talk on (Financial) Risk Model Validation. Two points:
- There's no point, indeed, in trying to falsify models, but they can be invalidated (for all kinds of reasons, and that might be temporary).
- Classical thinking about model validation (I usually show a diagram from a Schlesinger (1979) paper) starts with the modelling cycle:
Reality -> design -> conceptual model
Conceptual model -> implementation -> computerized model
Computerized model -> application -> reality
And it then accompanies the three steps with steps in the validation cycle:
Design <-> confirmation
Implementation <-> verification
Application <-> validation
So, validation in the narrow sense is dealing with actual use of an actual model implementation, which may be very different from intended use of a conceptual model (that would be dealt with in the confirmation step).