What The Law Of Large Numbers Really Means

JJ Couey, who hosts a podcast well known to some of you, and friend of the Broken Science Initiative, asked me about the so-called Law of Large Numbers. Jay wonders about sample sizes in experiments, or in observations, and says:

I really want to understand why bigger N doesn’t give you better results. If one just googles this idea, the law of large numbers is forced into your mind.

Short answer: the “law” applies to probability models, and not Reality, for nothing has a probability.

Long answer:

Let’s do the “law”, which I put in scare quotes one last time, not to emphasize its falsity, for it is true in its place, but to remind us that it applies to models, and has nothing to say, directly, about Reality.

The law has a strong and weak form. Both suppose that there exists an infinite sequence of something called “random variables”. Since this sequence is infinite, we already know we are talking about math somehow, and not Reality per se.

The idea of “random variables” is often made complex, but they are quite simple. Since “random” means unknown, and “variable” means takes more than one value, a “random variable” is an unknown value. The amount of money I have in my pocket now is, to you, a “random variable”, because that amount can vary, and you don’t know what it is. To me it is neither random nor variable, since I know it. Simple, as promised.

We can use math to quantify some probabilities. (Not all: ask me about this another day.) So we might suppose the uncertainty we have in our infinite sequence of random variables can be quantified by some parameterized probability distribution, which, in the law, has a parameter to represent it’s “expected value”. Which is sort of a center point (and a value that is not always expected in the English sense).

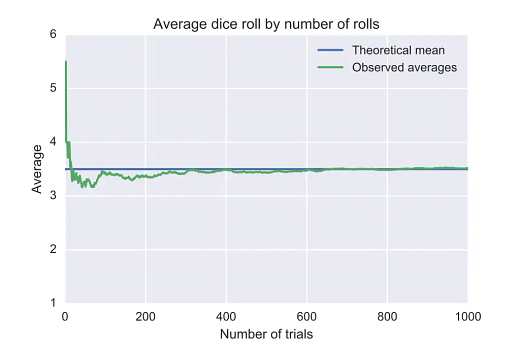
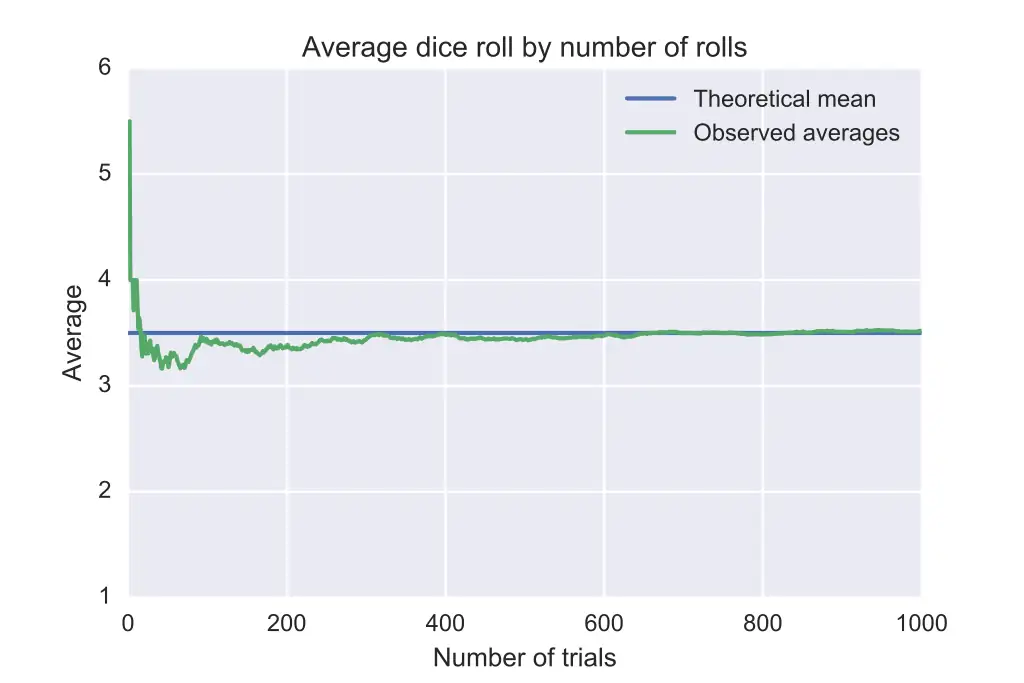
If we sum up a finite number of variables of this sequence, and divide by that finite number of the sum, that finite average converges in value to that parameter, in a mathematical sense, at infinity, which is a long way away.

That’s it! That’s the law.

Really, that’s it. There is a weaker version of the law, which uses that epsilon-delta business you may recall from your calculus days, to prove the same kind of thing. Mercifully, we’ll ignore this, since the differences are not important here.

Example? Before us is a device that may, and must, take one of m states, where each state has a cause of which we are ignorant. What is the probability, based on this evidence, and only this evidence, that the device is in state k? Where k is any of 1, 2, …, m. Right: 1/m.

The “expected value” is calculated by summing the value of each state multiplied by it’s probability. For this example, it’s 1 x (1/m) + 2 x (1/m) + … + m x (1/m) = [m x (m + 1)] / [2 x m]. If m = 6, then the expected value is 3.5. Which may look familiar to you.

So that, in math, an average of an infinite string of values of our mystery state must converge to [m x (m + 1)] / [2 x m].

In math, I say. What about a real device? One in Reality? Who knows! It may do anything. It may converge, it may diverge, it may catch fire and blow up. It may get stuck in one state and remain there forever. It may oscillate in some pattern we did not anticipate. It may do anything. Except operate indefinitely long.

The law is a model. Reality is on its own.

The law’s value to Reality is therefore the same as with any model. The closer that model represents Reality, the better the model will be. Reality, though, is not constrained by the model. Reality doesn’t know the model exists, because it doesn’t. The model is purely a product of our fevered imaginations. And nothing more. Which doesn’t make it bad—or good. It makes it a model.

Now some will say the law proves that as samples grow, the closer the mean of the same comes to the population mean. Pause a moment before reading further, for there is a flaw here.

The flaw is: who gets to choose the samples? Why are they samples? Why are these, and not other, observations collected together? Aha. Assumptions about cause are already being made in Reality! That’s how we pick samples in the first place. We pick things which we think have some of the same causes.

We’ve already seen coin flips don’t have a probability (nothing does) and can be caused to come up heads every time, if the causes are controlled.

That’s the first problem, that tacit or implicit knowledge of cause (in any of its four forms). Which people forget about. Causes may exist in the same way for each sample, or they may differ. It depends on how you take the sample. Which is why increasing a sample doesn’t necessarily bring you any closer to understanding what is going on. To do that, the better you control the causes, knowledge of which you (might) gain in taking the samples, the better you’ll do.

The second problem is that law says nothing about finite samples. But we don’t need the law to prove mean of samples from a finite population converge to the population mean in Reality. That is obviously true.

Suppose you want the average age of your friend’s sons. He has two. The first sample gives 5, which is the mean of one sample. The second sample gives you a mean of 7, which is also the population mean! Convergence has been reached, as expected. No law of probability was needed.

People often complicate these things by thinking immediately of hard cases, and go really wrong by adding the idea that probability has existence. Which it doesn’t.

The final answer of why increasing N doesn’t improve results is because cause is what we’re after, and cause is difficult. And Reality isn’t a model.

Subscribe or donate to support this site and its wholly independent host using credit card click here. Or use the paid subscription here. Cash App: $WilliamMBriggs. For Zelle, use my email: matt@wmbriggs.com, and please include yours so I know who to thank.