The Danish Mask Study Shows Masks Aren't Worth It

HUFFIN', PUFFIN' & BLUFFIN'

The blustery squid-stained panicked hersteric Nassim Nicholas Taleb---the man who called those who dared not run around screeching like teenage girls as he did at the start of the coronadoom panic "psychopaths"---a man who is a supreme 妈宝, a fact I include because Taleb likes language references---has claimed the Danish mask study which shows masks don't work ackshually shows masks do work, because math.

He's wrong.

Here is that study. They looked at two groups who stayed at least three hours outside their homes, with and without mask recommendations. The masked were supplied with "50 surgical masks and instructions for proper use." Which makes that group more rigorous than masks in the common public.

Goal: "The primary outcome was SARS-CoV-2 infection in the mask wearer at 1 month by antibody testing, polymerase chain reaction (PCR), or hospital diagnosis."

Outcome: "A total of 3030 participants were randomly assigned to the recommendation to wear masks, and 2994 were assigned to control; 4862 completed the study. Infection with SARS-CoV-2 occurred in 42 participants recommended masks (1.8%) and 53 control participants (2.1%)."

The completed numbers were 42/2392 mask infections vs. 53/2470 non-mask infections, where "infection" was defined generously, as you see.

Their conclusion: "The recommendation to wear surgical masks to supplement other public health measures did not reduce the SARS-CoV-2 infection rate among wearers by more than 50% in a community with modest infection rates, some degree of social distancing, and uncommon general mask use. The data were compatible with lesser degrees of self-protection."

I conclude, given the study's dictated rigorousness of mask usage ("good" ones supplied with proper instructions for use), and the generosity of noting an infection, and with all the other massive evidence we have about masks, that masks in the general public don't provide any significant benefit, or even no benefit, and can even cause harm.

Therefore making masklessness a crime, as many localities do, is asinine, anti-evidence, unethical, and immoral.

That's me. What about Taleb? Screams "Save me!" as usual. He starts his attack with these words:

Every study needs its own statistical tools, adapted to the specific problem, which is why it is a good practice to require that statisticians come from mathematical probability rather than some software-cookbook school. When one uses canned software statistics adapted to regular medicine (say, cardiology), one is bound to make severe mistakes when it comes to epidemiological problems in the tails or ones where there is a measurement error.

I am in near total agreement with this. Except for the very obvious caveat, which Taleb misses, that slavish adherence to math often leads to the Deadly Sin of Reification. Math misapplied is worse than no math, because it gives the false patina of "science." That, as it turns out, will be Taleb's mistake.

Now it should be obvious that the burden of proof is on Taleb and his Fearful Party and their petty tyrant instigators to show masks work. They are the ones insisting the masklessness is a crime.

It would therefore be an obvious and idiotic error to say that because this study says that masks don't work (as they defined "work") that therefore masks work because this study was incomplete. Right?

Taleb: "The study does not take into account the fact that masks might protect others."

So? The study also doesn't show that masks protects against gonorrhea in fleas. There are an infinite number of things the study doesn't show. What it does show is that wearing masks don't do much about protecting wearers from infection. If the other guy not wearing a mask is infected, you wearing one isn't going to do it for you. And anyway, they burden of proof is still on the Fearful Party to prove all claims about masks.

It's at this point Taleb launches into a blizzard of math, most of which is of no use, but which pleases the easily pleased. I will spare you (most of) the math, but assure you it is there and can be looked up.

THE EVIDENCE

There's two ways to look at this. We can assume perfection in the tests, or we can assume there's error in the form of both false positives and false negatives. Let's start with no error.

No Error

There was some missings (people entering the study but never measured). According to the "intention to treat" principle, we still have to account for them. Since the burden of proof is on the Fearful Party, it follows we should accord these missings as non-infections. In the same way as you count a non-response in a new drug trial as the drug not working. Fair is fair. But, since that makes my job too easy, I'll just ignore the missings, recalling that I'm then looking at a worst case scenario.

Taleb's binomial take is wrong in the sense that a better model exists, which, it turns out, regular readers met not that long ago. His binomial---and this will be hilarious for those who get the joke---is too small, too light in the tails! What a fun mistake.

We have evidence of 42/2392 mask infections vs. 53/2470 non-mask infections. We have to take that evidence as it is here assuming no error. And we want to extrapolate that information to Denmark as a whole.

We need only two assumptions: there are two states measured, infection or not, and a certain number of people measured. From that we deduce a beta-binomial predictive model (with deduced, i.e. know-with-certainty parameters) to extrapolate to those not yet measured (the math is all in here and in the many articles on the free stats class; all code is below at the bottom of this post). This is based on the prediction principle: I don't need to predict data I already know!

There are about 5.8 million Danes. We want the probability any number of them get infected whether or not they wear masks in the way prescribed (surgical, with training). This is easy. That is, we can calculate the probability of each possible outcome (0 new Danes infected, 1 new Dane infected, ..., 5.8 million new Danes infected) for both masks and no masks.

And then we can ask, given a person is infected, the chance they crap out. I don't know what the infection fatality rate of the coronadoom is in Denmark. They are, however, in no crisis as this Google picture search for "Denmark coronavirus deaths" shows.

Worldometer says Denmark has 146 doom deaths per million. And Ioannidis estimated counties with rates like that have an IFR of about 0.2%.

Since there is a possibility, however small, everybody wearing a mask or not can become infected, and we are ignoring all previous infections (accounting for them would only reduce the 5.8 million to some smaller number), we have to pick a probability cutoff.

For instance, we want to be 99% sure the number of infected will x or less, and solve for x for both masks and no masks. We can't use 100% certainty because that would give us 5.8 million for x for both groups (if you don't follow this, stop and think).

In our model, there is a 99% chance 144,185 or fewer masked would be infected, and 169,623 or fewer non-masked, out of 5.8 million. This is a difference of 25,438, which is the real effect we're looking for it the entire country mandated masks. This all assumes the model, data, full compliance, and so on.

Most people who get the doom have, at worst, mild symptoms. Therefore we want a more practical measure of its effect, such as deaths. This brings up the IFR. We assumed 0.2%. On average, given all our assumptions, we'd expect 0.002 * 25,438 = 51 (rounded up) lives would be "saved" by forcing all citizens to wear surgical masks with proper training. In our worst case scenario.

If we do intention to treat and realize most won't wear the masks as rigorously as the study prescribed, and some people aren't out of the house more than 3 hours a day, the real effect would be even smaller than 51 lives. Likely a lot smaller.

Error

Now let's bring in some error. We can have tests with a certain false positive and false negative rate. Opinions vary on the rates, but we know what they are here to a certain bound. How? Easy. Gaze and wonder at these glorious graphics.

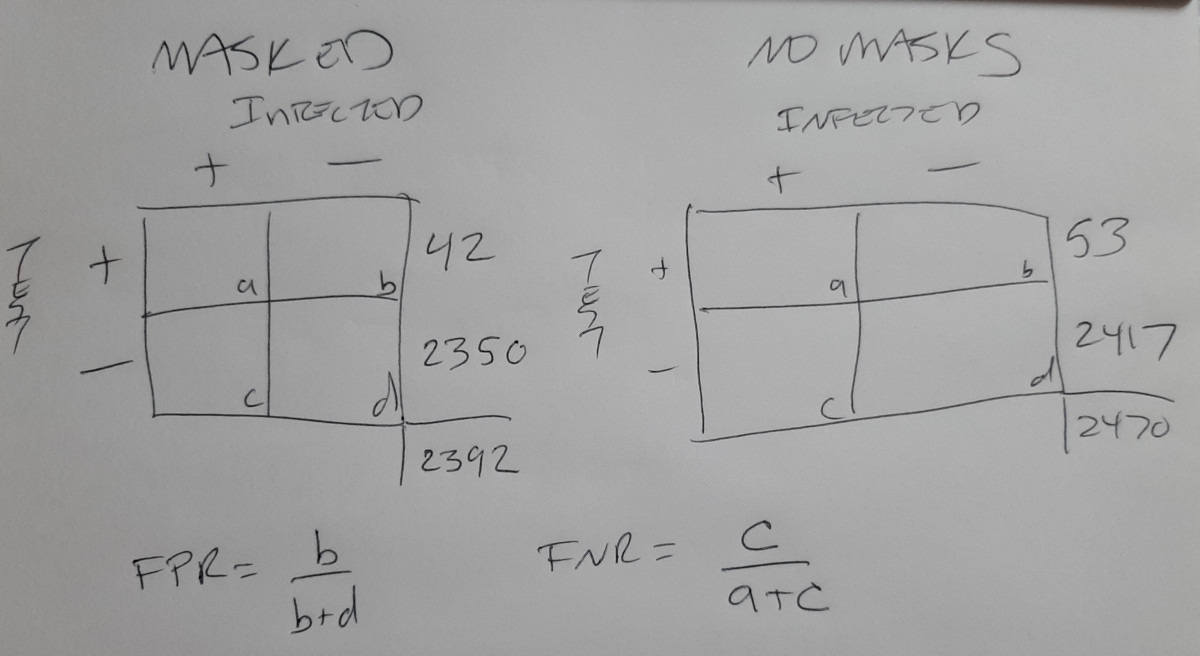
The cells are labeled to show that with the given marginal totals, we can solve for each cell value, as long as we know the error rates. We must accept the marginal totals, because that's what was measured!

For instance, a = c * (1 - FNR) / FNR, and b = d * FPR / (1 - FPR). We also have the constraints that c + d = 2350 (or 23417), and a + b = 42 (or 53). The latter may be written c * (1-FNR)/FNR + d * FPR/(1-FPR) = 42 (or 53). Given FPR and FNR, we then have two equations with two unknowns that can be solved for.

Taleb uses a FPR = 1%, so let's pick that with an equivalent FNR = 1%.

What we want is an estimate of the true infection rate. That would be ( a + c )/ n, with n = a + b + c + d = 2392 or 2370.

Plugging in 1% for both error rates gives (a + c) = 18 for masked, and 29 for unmasked. Notice these are smaller than the original 42 and 53 because of error: those 42 and 53 are positive tests, not actual infections if there's error.

We then repeat the same calculations as above, with 99% cutoffs. That gives a 99% chance no more than 73,930 infections in the masked group and 103,410 in the unmasked group. A difference of 29,480. Again, with an IFR of 0.2%, this is a difference of 59 bodies, rounded up.

So, as expected, the test error leads to more concern, but not much more. If we bump up the cutoff to 99.9%, we get a morgue count difference of 62. If we keep the 99% but double the FNR, in line with other estimates, we get a body count difference of 53 out of 5.8 million.

You can play with other plausible values, but the answers are all in the same ballpark. (There are some questions of limits of FPR and FNR with the given marginals, but we can ignore these here. You'll see the concerns if you push the rates too far away from 1%.)

Recall, again, this is the worst case scenario! Meaning the real effect will be less, even in the face of test error. Don't forget, beside all the other weakness, many have already been infected and won't be easily infected again soon, so the real number to consider is less than 5.8 million.

All these things and more will make the 53 smaller. And not only smaller, but much smaller.

IF WE CAN SAVE EVEN ONE LIFE!

The argument will be we must do everything we can to save even one life! This is a dumb argument, too dumb to even answer.

I went into nauseating detail, not so much to mock Taleb, though there is pleasure in that, but to help students interested in these things.

I do not ask you to take my model any more seriously than you take Taleb's. Because it has to be married to the great cache of evidence we already have about masks (link). It was clear before this study that there is no reason to mandate masks in the general public. With this study, it's even clearer.

To support this site and its wholly independent host using credit card or PayPal (in any amount) click here

CODE

I trust those who know how to play with code will figure this out.

newdbetabinom = function(x, n.new, k.old, n.old){
   # New observables for predictive distribution given:
   # k.old = observed "successes"
   # n.old = total old observations
   # x = vector of new totals, up to 0:n.new, or single x
   # n.new = number new observations expected
   # beta-binomial
   a = k.old+1
   b = n.old-k.old+1
   (ans = exp(lchoose(n.new,x)+lbeta(x+a,n.new-x+b)-lbeta(a,b)))
}
#############################
##
## NO ERROR
##
# masked and unmasked probabilities over 5.8 millions
s = 0:5.8e6 
m1e = newdbetabinom(s,max(s),   42,2392)
m0e = newdbetabinom(s,max(s),   53,2470)
# numbers of infected with probability cuttoff of 99%
# the "-1" is because the counts start at 0
(ni.1 = tail(which(cumsum(m1e) < 0.99),1)-1) # masked
(ni.0 = tail(which(cumsum(m0e) < 0.99),1)-1) # no masked
# different morgue counts with IFR = 0.002.
0.002 * (ni.0 - ni.1)
#############################
##
## ERROR
##
fpr = 0.01 # push this beyond 0.015 and watch the fur fly!
fnr = 0.01
a = c((1-fnr)/fnr, fpr/(1-fpr),
      1, 1)
a = matrix(a,nrow=2,byrow=T)
# masks
b = c(42, 2350)
r = solve(a,b)
(nti.1 = round(r[1]*(1 + (1-fnr)/fnr)))
# no masks
b = c(53, 2417)
r = solve(a,b)
(nti.0 = round(r[1]*(1 + (1-fnr)/fnr)))
s = 0:5.8e6
m1e = newdbetabinom(s,max(s),  nti.1,2392)
m0e = newdbetabinom(s,max(s),  nti.0,2470)
  
(ni.0 =  tail(which(cumsum(m0e) < 0.99),1)-1)
(ni.1 =  tail(which(cumsum(m1e) < 0.99),1)-1)
  
.002*(ni.0 - ni.1)

To support this site and its wholly independent host using credit card or PayPal (in any amount) click here