More Proof Hypothesis Testing Is Wrong & Why The Predictive Method Is The Only Sane Way To Do Statistics

Here it is, friends, the one complete universal simple function, the only function you will ever need to fit any---I said any---dataset x. And all it takes is one---I said one---parameter!

$latex f_{\alpha}(x) =\sin^2\left(2^{x\tau}\arcsin\sqrt{\alpha}\right) &s=4$.

Magnificent, ain't she? Toss away your regressions! Throw out your neural nets! Garbage your machine learning algorithms! This glorious little bit of math replaces them all!

Yes, sir, I do not idly boast. The function, the invention of one Laurent Boué, really does fit any set of data by it learning---they love this euphemism in computerland---that parameter α.

His paper is "Real numbers, data science and chaos: How to fit any dataset with a single parameter". Thanks to MA for the tip. Abstract (ellipses original):

We show how any dataset of any modality (time-series, images, sound...) can be approximated by a well-behaved (continuous, differentiable...) scalar function with a single real-valued parameter. Building upon elementary concepts from chaos theory, we adopt a pedagogical approach demonstrating how to adjust this parameter in order to achieve arbitrary precision fit to all samples of the data. Targeting an audience of data scientists with a taste for the curious and unusual, the results presented here expand on previous similar observations [1] regarding expressiveness power and generalization of machine learning models.

The magic parameter is α, which is "learned" (i.e. fit) from the data. The τ you set, and "is a constant which effectively controls the desired level of accuracy."

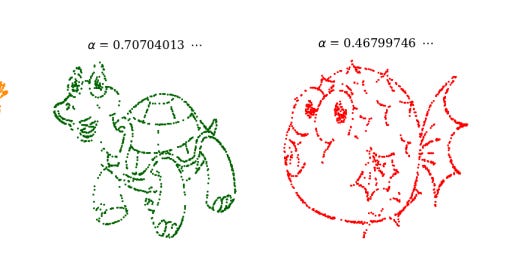
Before I show you how Boué's magic function shows hypothesis testing---wee p-values and all that---is wrong (which I don't believe he knew), here's some of the datasets he was able to fit by tuning α.

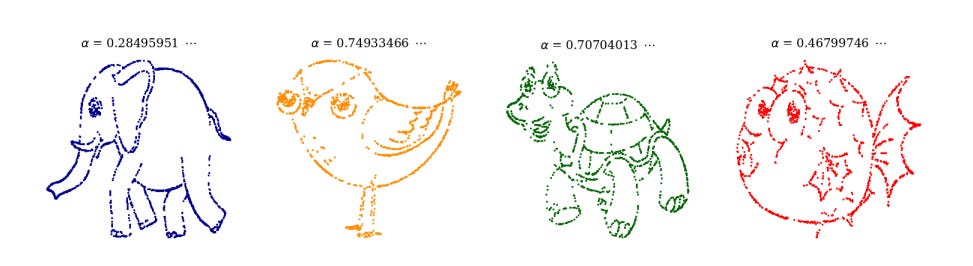
Nifty, eh?

Now this isn't a mathematical blog, so I won't pester you on how that parameter can be calculated. The explanation in the paper is clear and easy to read if you've had any training in these subjects. Boué even has code (at github) so all can follow along. Let's instead discuss the philosophy behind this.

First, this obvious picture. Before the dashed vertical line is the model fit in red; after the line is the model projection. The data is blue.

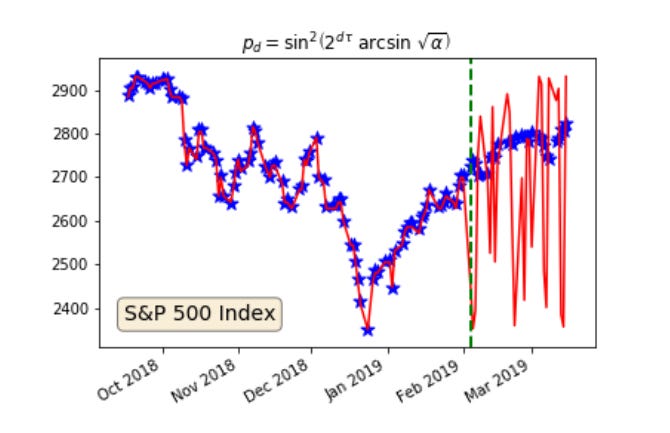
No surprise here. It has long been known that a function may be found to fit any dataset to arbitrary precision. What's new about this work is that we only need this and no other function to do those (over-)fits, and that the function needs only one parameter. Cool.

As is also known, fitting past data well is no guarantee whatsoever that the model will predict future data at all. The model may fit perfectly, but monkeys could do a better job guessing the unknown. Like in this example.

Ah, yes. That has been known. But what is surprising is that this knowledge is also proof that hypothesis testing is nonsense.

Maybe it's already obvious to you. If not, here's the thick detail.

The moment a classical statistician or computer scientist creates an ad hoc model, probability is born. Just like in It's A Wonderful Life with bells ringing and angels getting their wings. I do not mean this metaphorically or figuratively. It is literal.

It is, after all, what classical theory demands. Probability, in that theory, exists. It is as real as mass or electric charge. It is a ontic property of substances. And it has powers, causal powers. Probability makes things happen. I repeat: it exists. In that theory.

Granting this, and granting many of those who hold with the theory never remember it or think about its implications, it makes sense to speak of measuring probability. You can measure mass or charge, so why not probability? The data "contain" it. This is why frequentists, and even Bayesians and machine learners, speak of "learning" parameters (which must also exist and have "true" values), and of knowledge of "the true distribution" or the "data-generating distribution" (causal language alert!).

Hypothesis testing assumes the "true" probability on past data has been measured in some sense. If the model fit is good, the "null" hypothesis about the value of some "true"-really-exists probability parameter is rejected; if the fit is bad, it is accepted (though they use the Popperian euphemism "failed to be rejected"). The accepting or rejecting assumes the reality of the probability. You make an error when you accept the null but the "true" probability isn't what you thought.

Anyway, it's clear this universal function above will fit any data well. Null hypotheses will always be rejected if it is used, in the sense that the fit will always be excellent. The null that α = 0 will always be slaughtered. Your p-value will be smaller than Napoleon's on his way back from Moscow.

But the model will always predict badly. The fit says nothing about the ability to predict. The hypothesis test is thus also silent on this. Hypothesis testing is thus useless. Who needs to fit a model anyway, unless you want to make predictions with it?

Maybe that hasn't been noticed, because people sometimes pick models that aren't as bad as predicting as this function is. This not-so-bad model picking creates the false impress that the test has "discovered" something about the "true" probability.

No. The first test of any model is in how well it conforms to its premises, from which it is derived. The closer the premises are to be necessarily true, the closer the model is to Reality. The more the premises are ad hoc, the further it is.

This means the only practical test of an ad hoc good model is its ability to predict. Not how well it fits, as "verified" by a hypothesis test. How well it predicts. That, and nothing more.

Subscribe or donate to support this site and its wholly independent host using credit card or PayPal click here